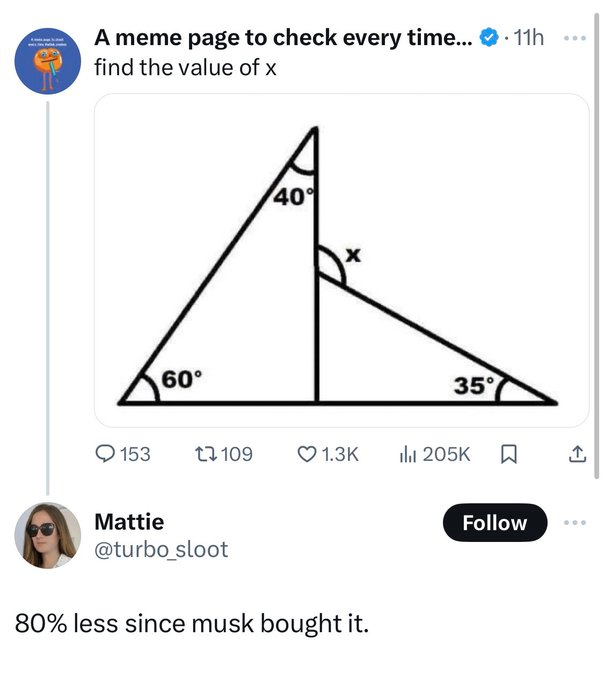
135° for anyone wondering.
correct, just commenting the 100/80 intersection looks like 90/90, i think it was intentionally misleading, classic trying to get you problem
What a bunch of bullshit. Just draw it way off 90 if you don’t want people to use a protractor. I calculated 125° because of this (but I’m happy I still got the right wrong answer, if that makes sense)
In my geometry classes, it’s only 90 degrees if it’s marked by a right angle marker. Otherwise, no matter how “right” it looks, if you assume before proving, it’s on you.
this is a meme tho. i wanted to treat it like a “real life” problem where if i saw those obviously 90 degree corners, i would just say it’s 90 because nowhere else in all my life outside of stupid schoolwork trick questions would that happen. which meant i got to the answer in a few seconds, which is a handy skill in real life.
You could potentially run into this or something very similar in cad when your sketches aren’t fully defined yet. I’ve definitely ran into models that are slightly off square because someone missed a constraint much earlier in the timeline.
Its not bullshit, its conventions that make a lot more whole sense later on.
Yes I originally thought 90 but then noticed the absence of a right angle sign. Also 60+40=100 which means the last angle should be 80. Making that perpendicular 100/80
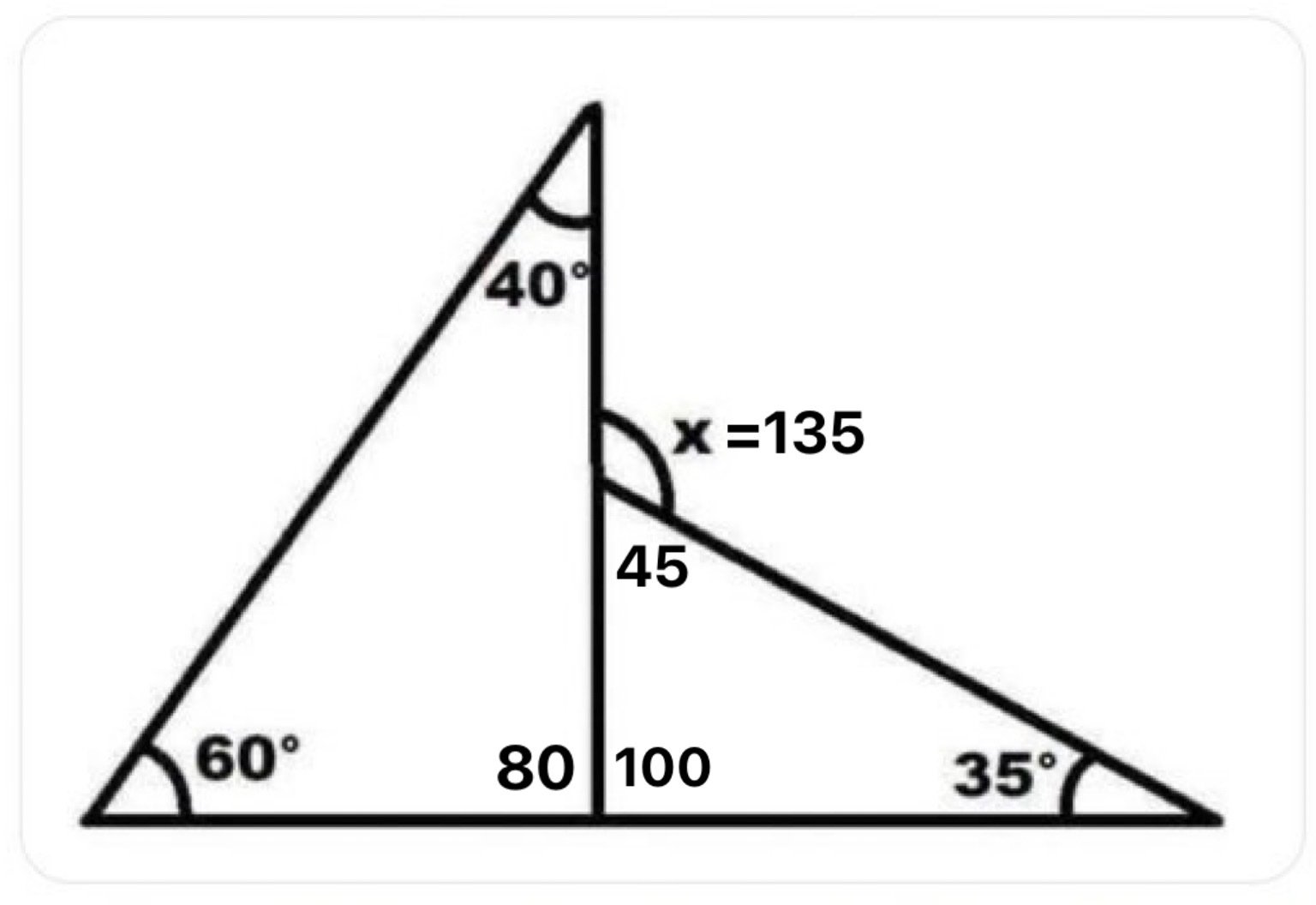
Yes, simple doodle below for anyone wondering.
You start from left, and calculate them 1 by 1, based on the angles that you already know. It is quite simple actually, you just have to know they always add up to 180 (within triangle, and when you “split” the space over a straight line).
you mean to say the right angles aren’t right angles? disgusting, get this outta my sight
evil math teacher laughing in background
this diagram does not provide a right angle indicator, and thus should not be assumed as a right angle
yes that’s the stupid excuse my math teacher would give
For context: it used to be 675° a few years back so the math checks out.
that’s not how global warming works
Nope. The value is “undefined”. You don’t have enough info to arrive at 135 - you are assuming that the bottom angle (sum of the angles that touch) is 180 degrees. Since there isn’t a datum saying the bottom “line” is straight, nor does it say the triangle on the right is an isosceles triangle, it is impossible to solve.
I don’t see any indication that this is limited to the Euclidean plane either
Haha, I love this.
Also nothing indicates the numbers are Arabic numerals.
You can’t prove it’s not hexadecimal.

I think assuming 2 line segments which make up a larger straight line segment to be parallel is generally accepted practice, and that would trump the angles that are drawn inaccurately.
Of course, it’d be better to put a hash through them both to indicate they’re parallel, especially given the deceptively drawn most-likely-not-a-right-angle.
deleted by creator
I got 125.
180-(90-35)=x 180-55=x 125=x
You’re assuming it is a right angle
Nothing states that it is
Even if it was a right angle, I think a second assumption is that the top left and bottom lines are equal length, which is also not stated.
I think there’s just not enough information in this picture to calculate the angle, and it can only be determined by measuring. But the image also does not specify that it is drawn to scale.
Oh shit you’re right. The left triangles unmarked angle is 80, meaning the right triangles internal angles are 100, 35, and 45. This means X is 135
It isn’t 90 degrees because the image is misleading. 60+40+y=180. y=80
I hated pictures like this in school. The numbers are just slapped on an inaccurate image and somehow they expect people to ignore the obvious right triangles and just focus on the math part of it.
Fun fact: In Turkey’s university admittance exam, all angles have to be absolutely accurate, and measurements have to be scaled down perfectly to the visible shape in a geometry question.
all angles have to be absolutely accurate
To what tolerance, though? Writing math exams has now become an engineering problem.
If it was to scale you could just use a protractor and skip the whole math part, which is the entire part of the lesson…
I don’t see that as a downside as long as these two questions are also included.
How many degrees make up the inner angles of a triangle?
How many degrees make up one side of a straight line?
Big assumption that the bottom line is straight / not two lines connecting at a different angle
And what’s wrong with that. Utilizing real world solutions to problems is a life skill. Not some obscure formula that you will forget anyway.
Adding and subtracting is a real life solution. Not sure how that is “obscure”
You are being obtuse. You know what I mean by obscure.
Its intended to focus on a specific skill, the other skill can be valid and not be the point of the lesson.
Then they could use decimals so it’s unlikely to get it right without calculating, 60.17°, 40.29°, 35.43°
If the student eventually does geometry for money, they’ll discover that customer CAD files invariably have some bizarre error like this.
I was scared I forgot basic trig stuff.
It’s even easier than going the triangle route.
A four-corner shape always has 360° internally.
So the internal angle of corner X is 360-(60+40+35).
The exterior angle therefore is 360-360-(60+40+35) = 60+40+35 = 135
That’s based on the assumption that the two angles in the middle add up to 180, which can’t be assumed by inspection alone as demonstrated by the visibly square 80° angle
No, you should completely ignore the bottom half of the center line. You end up with a shape with four turns. Those four internal angles always add to 360.
He is saying your shape might have 5 turns instead of 4 if the bottom line is not actually a line. Though if that was the case, the problem would not be solvable, so I doubt it.
Nice one, forgot this was an option too. You are missing a set of brackets though ;)
I love that every comment focus on the math puzzle. Since the other stuff is clearly uninteresting.